DspEdu 2.1 - "SPECTRA" Module

1. What does it do ?

This module calculates and displays Spectral Components of a periodic continuous-time waveform by evaluating FFT of a sampled and windowed sequence generated from the continuous-time waveform.

This module can be used to illustrate the resolution problem , spectral leakage problem and picket fence effect etc. in the context of spectral analysis of analog periodic waveforms using FFT. The module offers a choice of six windowing functions with a maximum window length of 256.

The sampled and windowed sequence can be saved into *.sp file in the default project directory. The spectral data output sequences also can be stored in *.txt file and the plots can be saved in *.ps (Postscript Format) files in the default project directory.

The program allows various options to display the FFT in polar or rectangular form in drop line or curve modes.

2. Tab Windows

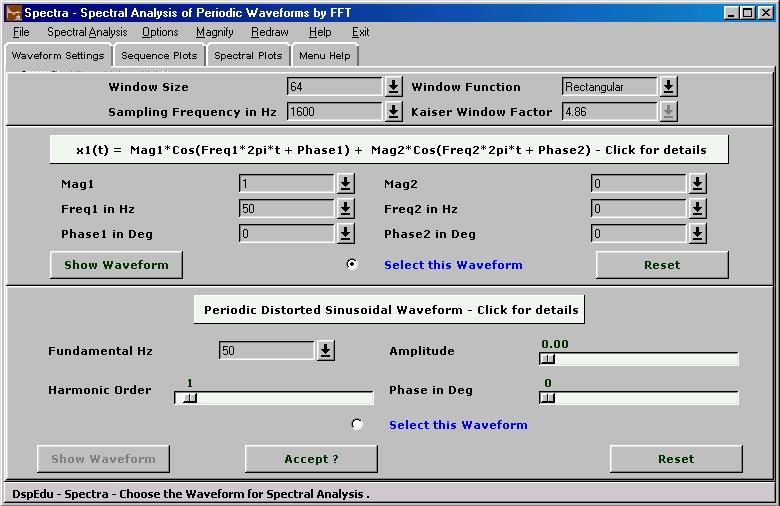
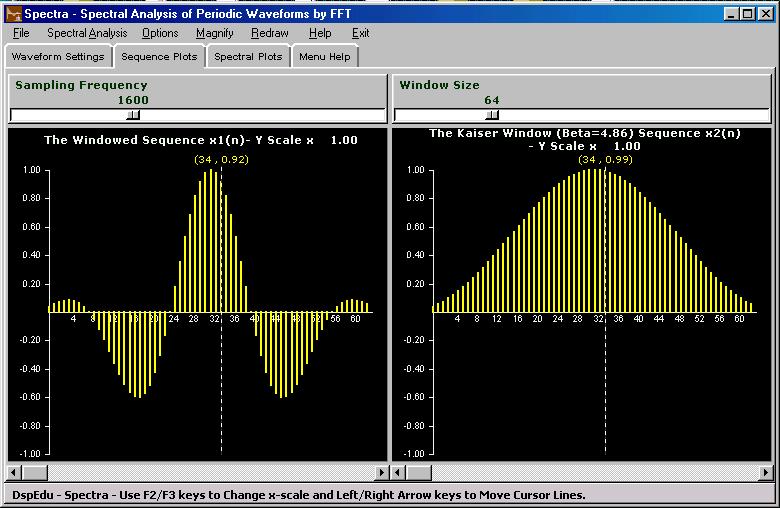
2.1 'Waveform Settings' Window

Allows the generation of the waveforms for carrying out spectral analysis on. Two kinds of waves can be constructed from here. the first one is a sum of two sinusoids with same or different amplitudes,frequencies and phases.You can select the parameters from the pull-down boxes or type in the desired values.Useful for resolution and spectral leakage studies.Study the effect of Window Length , Window Parameter,DFT Length etc on the reported spectrum.selection of frequency and phase parameters of the two sinusoids in the periodic wave, the sampling frequency , the window length , shape and window parameter etc.

The second kind is a distorted Sinusoidal Periodic Wave with amplitude and phase of all harmonics upto 25th individually settable.Click on the waveform selection radio button and set the fundamental frequency first.Then choose the harmonic order and set the amplitude and phase for this component by using the slider scales for the purpose.Once the desired values are set in the scale press 'Accept' button to enter the component.Proceed with other harmonic components similarly.

Once all the desired components are accepted press the 'Show Waveform' button or raise the 'Sequence Plots' window. The value of fundamental frequency used will be the value that appears in the entry box for it at the time you press the 'Show Waveform' button or when you raise the 'Sequence Plots' window.Your current harmonic data remains current till you press the 'Reset' button here. The currently accepted components can be examined by selecting the corresponding harmonic order in the slider scale ; the corresponding amplitude and phase will appear in the relevant slider scale units.

Harmonic Analysis of 50Hz Utility Current and Voltage waveforms is an important FFT application area in Electrical Power Systems and Industrial Electronics.You can study the effect of window length , DFT length , Synchronised Vs Asynchronous Sampling etc in such applications using the waveforms synthesised from here.

2.2 'Sequence Plots' Window
Shows the sampled and windowed sequence alongwith the window sequence used as per the current parameters in the 'Waveform Settings' window. Each plot is associated with a slider scale. Clicking on the slider and moving it changes the corresponding parameter and the plots are updated immediately. Also the entries in the 'Waveform Settings' window will track the slider movements.

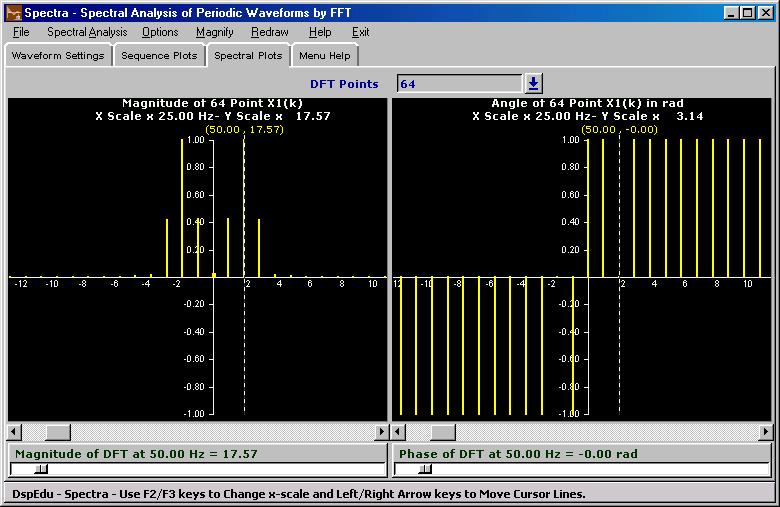
2.3 'Spectral Plots' Window
Shows the two-sided spectral plots (when the window is raised calculates FFT and updates the plots if necessary) of the waveform currently on display in the 'Sequence Plots' window. Shows Magnitude and Angle by default. It is possible to display in Rectangular form by option change. Shows Drop Lines plot by default. The window also includes a 'DFT Points' entry box which contains a selected value which is equal to window length by default. Different values upto 512 may be selected and FFT will be recalculated and plots updated whenever a different value is selected in the box.
Two slider scales appearing at the bottom of the plots allow readout of index and spectral data at that index. Magnitude spectra will have even symmetry and Angle spectra will have odd symmetry. Hence the slider scales cover only one side of the spectra.

2.4 'Menu Help' Window
Raises the window and puts a brief help on the menu items in it.

3. Menubar Items

3.1 File Menu

3.1.1 Load Saved Project

Load a Sampled & Windowed Sequence and the Window Sequence used by opening a *.sp file saved in an earlier session.The default directory will be '/Projects/spectra'

3.1.2 Save Project
Brings up a standard Windows Save Dialog box which opens into '/Projects/spectra' by default and shows *.sp as the default extension.The number of points in the sequences and sequence data will be stored as an ascii file with selected name and 'sp' extension.The program assumes write permission in the chosen directory , overwrites with prompt and does not provide confirmation dialog.

3.1.3 Save Spectral Data
Brings up a standard Windows Save Dialog box which opens into '/Projects/spectra' by default and shows *.txt as the default extension. The number of points in the sequences, the sequence data , FFT output data etc.will be stored as an ascii file with selected name and 'txt' extension. The number of points calculated in FFT will be as per the current values in 'DFT Points' box in the Spectral Plots Page. The program assumes write permission in the chosen directory , overwrites with prompt and does not provide confirmation dialog.

3.1.4 Save Plots
Brings up a standard Windows Save Dialog box which opens into '/Projects/spectra' by default and shows *.ps as the default extension.The four plots which currently appear in the four plot areas will be saved as four postscript files with selected names and 'ps' extension. The number of points calculated in Spectral data will be as per the current values in 'DFT Points' box . The program assumes write permission in the chosen directory , overwrites with prompt and does not provide confirmation dialog.

3.2 Spectral Analysis Menu

3.2.1 Show X1(k)
Carries out the FFT Computation for Windowed Sequence and plots the result in spectral plot area in two-sided version. The number of DFT Coefficients calculated will be as per the current entry in the DFT Points box and is equal to the window legth to begin with. Magnitude and Angle are plotted by default. Option to plot the real part and imaginary part is available under the Options menu.

3.2.2 Show X2(k)
Carries out the FFT Computation for the Window Sequence used in the spectral analysis and plots the result in spectral plot area in two-sided version. The number of DFT Coefficients calculated will be as per the current entry in the DFT Points box and is equal to the window legth to begin with. Magnitude and Angle are plotted by default. Option to plot the real part and imaginary part is available under the Options menu.

3.3 Options

3.3.1 Spectral Display Options

Polar Form - Show DFT Coefficients or Fourier Transform in Polar Form. This is the default.

3.3.2 Display Mode

3.3.2 Numeric Result Windows Enable/Disable

3.3.4 Display Color Options

3.4 Magnify

3.5 Redraw

3.6 Help

3.7 Exit

4. Restrictions in the Evaluation Version

5. Author